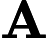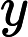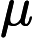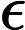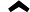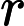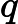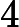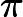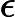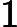Function Conjunction → Electromagnetic Potentials

From S.H.O.
Revision as of 21:08, 15 March 2017 by S.H.O. (Talk | contribs) (→‎Explaining Cyril Smith's "Marinov Generator" using standard Lorentz Transforms)

Jump to: navigation, search

The basic idea here is that the electromagnetic potentials [math]\varphi[/math] and [math]A[/math] may be the underlying key to several inventions related to electromagnetic forces.

Introduction

From December 2016 to March 2017, I (S.H.O. talk) have been conducting electromagnetic simulations using JavaScript and the THREE.js script library (http://threejs.org). Based on these results, I have determined that the magnetic component of the Lorentz force:

[math]\mathbf{F_{mag}} = q\ \mathbf{v} \times \mathbf{B} = q\ \left[ \nabla_\mathbf{A}(\mathbf{v}\cdot\mathbf{A}) - (\mathbf{v}\cdot\nabla)\mathbf{A} \right] [/math]

causes transfers of energy within the magnetic rotor assembly (such as electron kinetic energy and inductive storage energy into wire kinetic energy (wired rotor example), or atomic electron kinetic energy to magnetic domain kinetic energy (permanent magnet rotor example)) that, in the low-frequency approximation, pretty much matches the amount of energy transfer between fields and the driving (stator) coils which is due to the transformer induction electric field [math]- \frac{\partial \mathbf{A}}{\partial t}[/math] acting on currents in the coils from the relative motion of the magnetic rotor assembly.

As a result, the only way using conventional physics to explain various devices, such as the Marinov Motor[1], the Distinti Paradox2[2], and, especially, the Marinov Generator[3][4] is to more accurately define the electric field [math]\mathbf{E}[/math], which is part of the full Lorentz Force equation, and then see if it leads to predictions that confirm observations, especially those found figure 9 of Cyril Smith's 2009 paper on the "Marinov Generator".[4] S.H.O. talk 22:09, 5 March 2017 (PST)

Prior content in the "Comment Record" section:

Prior content in the "Background" section:

http://www.sho.wiki/index.php?title=Electromagnetic_Potentials&diff=next&oldid=1162

Novel Force laws proposed by various researchers

Stefan Marinov's proposal

Stefan Marinov proposed adding the "motional-transformer induction" on charge q:[5]

[math](\mathbf{v_{wire}}\cdot\nabla)\mathbf{A}[/math]

or rather:

[math]-(\mathbf{v_{charge}}\cdot\nabla)\mathbf{A}[/math]

to the Lorentz force.

The extra term is equivalent to:[6]

[math]-(\mathbf{v}\cdot\nabla)\mathbf{A} = \begin{matrix} - \left[ v_x \frac{∂A_x}{∂x} + v_y \frac{∂A_x}{∂y} + v_z \frac{∂A_x}{∂z} \right] \mathbf{e}_x \\ - \left[ v_x \frac{∂A_y}{∂x} + v_y \frac{∂A_y}{∂y} + v_z \frac{∂A_y}{∂z} \right] \mathbf{e}_y \\ - \left[ v_x \frac{∂A_z}{∂x} + v_y \frac{∂A_z}{∂y} + v_z \frac{∂A_z}{∂z} \right] \mathbf{e}_z \end{matrix}[/math]

Where [math]\mathbf{v}[/math] is the velocity of the charge.

The Lorentz force is:

[math]\mathbf{F} = q\left[-\nabla \varphi- \frac{\partial \mathbf{A}}{\partial t}+ \nabla_\mathbf{A}(\mathbf{v}\cdot\mathbf{A})-(\mathbf{v}\cdot\nabla)\mathbf{A} \right][/math]

Therefore, adding the extra term proposed by Stefan Marinov results in:

[math]\mathbf{F} = q\left[-\nabla \varphi- \frac{\partial \mathbf{A}}{\partial t}+ \nabla_\mathbf{A}(\mathbf{v}\cdot\mathbf{A})-2(\mathbf{v}\cdot\nabla)\mathbf{A} \right][/math]

The problem with this modification:

In the case of an electrical charge approaching a wire, this additional term proposed by Marinov doubles the force of deflection. This is not observed.

Consider the vector potential due a current-carrying wire on the x-axis. Both the current and the vector potential of this current point in the +x direction. Now have a charge approaching this wire perpendicularly. Both the magnetic Lorentz force and the additional Marinov term predict the same force.

Now consider the case where the wire is moving toward the charge. In this case, both the transformer induction [math]- \frac{\partial \mathbf{A}}{\partial t}[/math] and the additional Marinov term predict the same force acting on the charge directed parallel to the vector potential of the current. The term proposed by Marinov doubles the observed force in these cases.

Cyril Smith's proposal

Cyril Smith proposed adding the following gradient to the Lorentz force:[3]

[math]- \nabla_\mathbf{A}(\mathbf{v}\cdot\mathbf{A})[/math]

This is equal to:

[math]- \nabla_\mathbf{A}(\mathbf{v} \cdot \mathbf{A}) = \begin{matrix} - \left[ v_x \frac{∂A_x}{∂x} + v_y \frac{∂A_y}{∂x} + v_z \frac{∂A_z}{∂x} \right] \mathbf{e}_x \\ - \left[ v_x \frac{∂A_x}{∂y} + v_y \frac{∂A_y}{∂y} + v_z \frac{∂A_z}{∂y} \right] \mathbf{e}_y \\ - \left[ v_x \frac{∂A_x}{∂z} + v_y \frac{∂A_y}{∂z} + v_z \frac{∂A_z}{∂z} \right] \mathbf{e}_z \end{matrix}[/math]

The idea behind this was to explain an observation in an experiment involving a "Marinov Generator"[3] in which longitudinal induction forces were produced.

The Lorentz force is:

[math]\mathbf{F} = q \left[ -\nabla \varphi - \frac{\partial \mathbf{A}}{\partial t} + \nabla_\mathbf{A}(\mathbf{v}\cdot\mathbf{A}) - (\mathbf{v}\cdot\nabla)\mathbf{A} \right][/math]

Therefore, adding the extra term proposed by Cyril Smith results in:

[math]\mathbf{F} = q \left[ -\nabla \varphi - \frac{\partial \mathbf{A}}{\partial t} + 0\nabla_\mathbf{A}(\mathbf{v}\cdot\mathbf{A}) - (\mathbf{v}\cdot\nabla)\mathbf{A} \right][/math]

The problem with this modification:

In the case of two parallel current-carrying wires, this additional term proposed by Cyril Smith negates the magnetic forces between the currents. It turns out that the extra term may yield forces perpendicular to the velocity. The relevant field components are:

[math]- \nabla_\mathbf{A}(\mathbf{v} \cdot \mathbf{A})_\bot = \begin{matrix} - \left[ v_y \frac{∂A_y}{∂x} + v_z \frac{∂A_z}{∂x} \right] \mathbf{e}_x \\ - \left[ v_x \frac{∂A_x}{∂y} + v_z \frac{∂A_z}{∂y} \right] \mathbf{e}_y \\ - \left[ v_x \frac{∂A_x}{∂z} + v_y \frac{∂A_y}{∂z} \right] \mathbf{e}_z \end{matrix}[/math]

Explaining the Marinov Motor and Cyril Smith's "Marinov Generator" using Conventional Physics

The Longitudinal E-field derived from the Liénard–Wiechert Potentials

Believe it or not, the electromagnetic potentials formulated independently by Alfred-Marie Liénard[7] and Emil Wiechert[8] anticipate an electric field with longitudinal components.

The Liénard–Wiechert potentials [math]\varphi[/math] (scalar potential field) and [math]\mathbf{A}[/math] (vector potential field) are for a source point charge [math]q[/math] at position [math]\mathbf{r}_s[/math] traveling with velocity [math]\mathbf{v}_s[/math]:

[math]\varphi(\mathbf{r}, t) = \frac{1}{4 \pi \epsilon_0} \left(\frac{q}{(1 - \mathbf{n} \cdot \boldsymbol{\beta}_s)|\mathbf{r} - \mathbf{r}_s|} \right)_{t_r}[/math]

and

[math]\mathbf{A}(\mathbf{r},t) = \frac{\mu_0c}{4 \pi} \left(\frac{q \boldsymbol{\beta}_s}{(1 - \mathbf{n} \cdot \boldsymbol{\beta}_s)|\mathbf{r} - \mathbf{r}_s|} \right)_{t_r} = \frac{\boldsymbol{\beta}_s(t_r)}{c} \varphi(\mathbf{r}, t)[/math]

where [math]\boldsymbol{\beta}_s(t) = \frac{\mathbf{v}_s(t)}{c}[/math] and [math]\mathbf{n} = \frac{\mathbf{r} - \mathbf{r}_s}{|\mathbf{r} - \mathbf{r}_s|}[/math].

The electric field derived from this is:

[math]\begin{align}\mathbf{E}(\mathbf{r}, t) = \frac{q}{4 \pi \epsilon_0} \frac{1}{|\mathbf{r} - \mathbf{r}_s|^2(1 - \mathbf{n} \cdot {\boldsymbol \beta}_s)^3} \left[\left(\mathbf{n} - {\boldsymbol \beta}_s\right)(1-{\beta_s}^2) + |\mathbf{r} - \mathbf{r}_s|(\mathbf{n} \cdot \dot{\boldsymbol \beta}_s/c) (\mathbf{n} - {\boldsymbol \beta}_s) - |\mathbf{r} - \mathbf{r}_s|\big(\mathbf{n} \cdot (\mathbf{n} - {\boldsymbol \beta}_s)\big) \dot{\boldsymbol \beta}_s/c \right]\end{align}[/math]

which is equal to [math]-{\boldsymbol \nabla}\varphi - \frac{d\mathbf{A}}{dt}[/math]

If acceleration [math]\dot{\boldsymbol \beta}_s[/math] is small, then we have:

[math]\begin{align}\mathbf{E}(\mathbf{r}, t) = \frac{q}{4 \pi \epsilon_0} \frac{1}{|\mathbf{r} - \mathbf{r}_s|^2(1 - \mathbf{n} \cdot {\boldsymbol \beta}_s)^3} \left(\mathbf{n} - \hat{{\boldsymbol \beta}}_s\right)(1-{\beta_s}^2)\end{align}[/math]

If [math]\mathbf{n}[/math] is parallel to [math]{\boldsymbol \beta}_s[/math], then:

[math]\mathbf{E}(\mathbf{r}, t) = \frac{q}{4 \pi \epsilon_0} \frac{1}{|\mathbf{r} - \mathbf{r}_s|^2(1 - \beta_s)^3} \left(\mathbf{n} - {\boldsymbol \beta}_s\right)(1 - {\beta_s}^2)[/math]
[math]\mathbf{E}(\mathbf{r}, t) = \frac{q}{4 \pi \epsilon_0} \frac{1}{|\mathbf{r} - \mathbf{r}_s|^2(1 - \beta_s)^3} \left(\mathbf{n} - {\boldsymbol \beta}_s\right)(1 - \beta_s)(1 + \beta_s)[/math]
[math]\mathbf{E}(\mathbf{r}, t) = \frac{q}{4 \pi \epsilon_0} \frac{1}{|\mathbf{r} - \mathbf{r}_s|^2(1 - \beta_s)^2} \left(\mathbf{n} - {\boldsymbol \beta}_s\right)(1 + \beta_s)[/math]

If in addition to the aforementioned condition, the condition [math]|{\boldsymbol \beta}_s| \ll |\mathbf{n}|[/math] is also satisfied, then we can approximate [math]\mathbf{\hat{n}} - \hat{{\boldsymbol \beta}}_s[/math] as [math]\mathbf{\hat{n}}[/math]. This affects only the direction of the calculated electric field, not its magnitude. Regarding the instance of [math]\left(\mathbf{n} - {\boldsymbol \beta}_s\right)[/math], what we can do is factor out the magnitude [math]|\mathbf{n} - {\boldsymbol \beta}_s|[/math] from the vector, and the use the approximation from the unit vector. Note, remember that [math]\mathbf{n}[/math] and [math]{\boldsymbol \beta}_s[/math] were taken to be co-linear. Therefore:

[math]\mathbf{E}(\mathbf{r}, t) = \frac{q}{4 \pi \epsilon_0} \frac{1}{|\mathbf{r} - \mathbf{r}_s|^2(1 - \beta_s)^2} \mathbf{\hat{n}} \left(1 - \beta_s\right)(1 + \beta_s)[/math]
[math]\mathbf{E}(\mathbf{r}, t) = \frac{q}{4 \pi \epsilon_0} \frac{1}{|\mathbf{r} - \mathbf{r}_s|^2(1 - \beta_s)^2} \mathbf{\hat{n}} (1 + \beta_s)[/math]
[math]\mathbf{E}(\mathbf{r}, t) = \frac{q}{4 \pi \epsilon_0} \frac{1}{|\mathbf{r} - \mathbf{r}_s|^2} \frac{1 + \beta_s}{1 - \beta_s} \mathbf{\hat{n}}[/math]

Recognizing that the above condition limits the situation to non-relativistic velocities, that is to say [math]{\boldsymbol \beta} \ll 1[/math] or [math]|\mathbf{v}_s| \ll c[/math], then we can approximate [math]1 - \beta_s[/math] as [math]1[/math] without significantly affecting the numerator [math]1 + \beta_s[/math]. Therefore:

[math]\mathbf{E}(\mathbf{r}, t) = \frac{q}{4 \pi \epsilon_0} \frac{1 + \beta_s}{|\mathbf{r} - \mathbf{r}_s|^2} \mathbf{\hat{n}}[/math]

The "rigid" contribution to the electric field is:

[math]\mathbf{E}(\mathbf{r}, t)_{rigid} = \frac{q}{4 \pi \epsilon_0} \frac{1}{|\mathbf{r} - \mathbf{r}_s|^2} \mathbf{\hat{n}}[/math]

If we consider an electromagnetic device composed of electrically neutral objects, what remains is a "quasistatic" contribution to the electric field.

[math]\mathbf{E}(\mathbf{r}, t)_{quasistatic} = \frac{q}{4 \pi \epsilon_0} \frac{\beta_s}{|\mathbf{r} - \mathbf{r}_s|^2} \mathbf{\hat{n}}[/math]

Given that:

[math]\mathbf{A}(\mathbf{r},t) = \frac{\boldsymbol{\beta}_s(t_r)}{c} \varphi(\mathbf{r}, t)[/math]

We can substitute for [math]\beta_s[/math]:

[math]|\mathbf{A}(\mathbf{r},t)|c = \beta_s \varphi(\mathbf{r}, t)[/math]
[math]\beta_s = \frac{|\mathbf{A}(\mathbf{r},t)|c}{\varphi(\mathbf{r}, t)}[/math]

Because this scenario considers non-relativistic velocities, that is to say [math]{\boldsymbol \beta} \ll 1[/math] or [math]|\mathbf{v}_s| \ll c[/math], we can again approximate the denominator. Therefore:

[math]\beta_s = \frac{|\mathbf{A}(\mathbf{r},t)|c}{\frac{q}{4 \pi \epsilon_0} \frac{1}{|\mathbf{r} - \mathbf{r}_s|}}[/math]

Therefore, substitution for [math]\beta_s[/math] gives:

[math]\mathbf{E}(\mathbf{r}, t)_{quasistatic} = \frac{q}{4 \pi \epsilon_0} \frac{1}{|\mathbf{r} - \mathbf{r}_s|^2} \frac{|\mathbf{A}(\mathbf{r},t)|c}{\frac{q}{4 \pi \epsilon_0} \frac{1}{|\mathbf{r} - \mathbf{r}_s|}} \mathbf{\hat{n}}[/math]
[math]\mathbf{E}(\mathbf{r}, t)_{quasistatic} = \frac{|\mathbf{A}(\mathbf{r},t)|c}{|\mathbf{r} - \mathbf{r}_s|} \mathbf{\hat{n}}[/math]

Force is four-dimensional, not three dimensional

A New Idea: The Makerarc

The above result supports a development beyond the S.H.O. Drive. A much more powerful and compact permanent magnet system is now envisioned, the viability of which rests on the condition that [math]\langle \nabla \varphi' \rangle = 0[/math] on each charge [math]q[/math]. The preliminary name is Makerarc (MAY-KERR-ARK), which stands for:

  • Magnetic
  • Atom
  • Kinetic
  • Energy
  • Reservoir
  • And
  • Resource
  • Channel

Details pending. Stay tuned. Sincerely, S.H.O. talk 22:09, 5 March 2017 (PST)

Explaining "Reduced-Lenz" Devices

It is anticipated that the above stated condition [math]\langle \nabla \varphi' \rangle = 0[/math] which leads to the electric field [math]- |\mathbf{v}| \nabla A_\parallel[/math] may explain some types of Reduced-Lenz devices. A good example can be found in the video below ("Ray's No Back EMF Generator"):

Simulations in JavaScript and THREE.js have determined that in many cases the magnetic Lorentz force [math]q\ \mathbf{v} \times \mathbf{B}[/math] will be opposed in part by the additional force [math]q \left[ - |\mathbf{v}| \nabla A_\parallel \right][/math]. This makes certain types of magnetic circuit arrangements more efficient at electrical power generation (in terms of output power vs. input power) but less efficient as an electrical motor. Simulations of the S.H.O. Drive indicated that the additional force may vary between assisting or opposing the magnetic Lorentz force, which is helpful depending on whether the goal is to develop an efficient motor or an efficient generator, respectively. The simulated S.H.O. Drive designs appeared to switch between these two extremes every quarter cycle. The only way to make it work would have been to increase the inductive reactance (so that the current would be delayed by about a quarter cycle), and even then, simulations indicated that the extra term was typically insufficient to completely reverse the net force. However simulations of various rotor and S.H.O. coil curve modifications for the S.H.O. Drive showed that it was possible for the additional force to be a significant percentage of the magnetic Lorentz force. Per more recent simulations (early March), the Makerarc design (previous section) will improve upon this many fold, unless if permanent magnets do not permit the [math]\langle \nabla \varphi' \rangle = 0[/math] condition. S.H.O. talk 23:39, 5 March 2017 (PST)

Explaining the Newman Motor

A Newman Motor-style coil and magnet arrangement, like that shown in the video below, have been simulated by me using JavaScript and THREE.js.

The extra electric field term [math]- |\mathbf{v}| \nabla A_\parallel[/math] based on the condition [math]\langle \nabla \varphi' \rangle = 0[/math] predicts a significant opposition to the magnetic Lorentz force at angles slightly straying from the "top-dead-vertical" position, making it a better generator than a motor. However, when energy is discharged from the "generator coil" to the "motor coil" of Newman's motor, the rotor will have often changed position to the point where the magnetic Lorentz force becomes increasingly significant, helpful for motive purposes. Newman's motor operated at a high Q, which facilitated energy recovery. S.H.O. talk 00:00, 6 March 2017 (PST)

References

  1. ↑ http://redshift.vif.com/JournalFiles/Pre2001/V05NO3PDF/v05n3phi.pdf
  2. ↑ http://www.distinti.com/docs/pdx/paradox2.pdf
  3. ↑ 3.0 3.1 3.2 http://overunity.com/14691/the-marinov-generator/
  4. ↑ 4.0 4.1 http://www.overunityresearch.com/index.php?action=dlattach;topic=2470.0;attach=13897
  5. ↑ https://archive.org/stream/thornywayoftruthpart4maririch#page/104/mode/2up/search/motional-transformer+induction
  6. ↑ http://www.overunityresearch.com/index.php?action=dlattach;topic=2470.0;attach=13908
  7. ↑ https://docs.google.com/file/d/0B817m31MAj0wZTZjZmMwMjgtY2Y5YS00YTQ5LThjM2EtNzhjYTYzNzFlZDY0/edit?hl=en_GB&pli=1
  8. ↑ https://docs.google.com/file/d/0B817m31MAj0wMDI1YjllYjctY2NhOS00M2M2LWFlMTUtYjVmYTkyZmVlY2M2/edit?hl=en_GB

See also

Site map

HQ ● Glossary ● April 2016 Presentation

Retrieved from "http://www.sho.wiki/index.php?title=Electromagnetic_Potentials&oldid=1579"