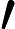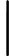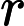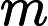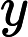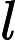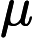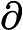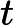Function Conjunction → Functions composed of Physical Expressions

Functions for a point charge $q'$

The electric scalar potential $\mathbf{\varphi}$ at $\left(\mathbf{r},t\right)$ due to a point charge $q'$ at $\left(\mathbf{r'},t'\right)$ is:

$\mathbf{\varphi}\left(\mathbf{r},\mathbf{r'}\right) \quad = \quad \underset{constant}{\frac{q'}{4\pi\ \epsilon_0}} \quad \underset{proximity}{\frac{1}{|\mathbf{r}-\mathbf{r'}|}}$

The magnetic vector potential $A$ at $\left(\mathbf{r},t\right)$ due to a point charge $q'$ which had a velocity $\frac{∂\mathbf{r'}}{∂t}$ at $\left(\mathbf{r'},t'\right)$ is:

$\mathbf{A}\left(\mathbf{r},\mathbf{r'}\right) \quad = \quad \mathbf{\varphi}\left(\mathbf{r},\mathbf{r'}\right) \quad \underset{constant}{\frac{1}{c^2}} \quad \underset{dislocation}{\frac{∂\mathbf{r'}}{∂t}}$

$\mathbf{A}\left(\mathbf{r},\mathbf{r'}\right) \quad = \quad \underset{constant}{\frac{\mu_0\ q'}{4\pi}} \quad \underset{proximity}{\frac{1}{|\mathbf{r}-\mathbf{r'}|}} \quad \underset{dislocation}{\frac{∂\mathbf{r'}}{∂t}}$

Functions for an ordered pair of point charges $(q,q')$

A charge $q$ subject to an electric scalar potential $\varphi$ at $\left(\mathbf{r},t\right)$ due to a point charge $q'$ at $\left(\mathbf{r'},t'\right)$ has an electric potential energy of:

q φ (r, r^{'}) = \underset{c o n s t a n t}{\frac{q q^{'}}{4 π ϵ_{0}}} \underset{p r o x i m i t y}{\frac{1}{| r - r^{'} |}}

$q\varphi\left(\mathbf{r},\mathbf{r'}\right) \quad = \quad \underset{constant}{\frac{qq'}{4\pi\ \epsilon_0}} \quad \underset{proximity}{\frac{1}{|\mathbf{r}-\mathbf{r'}|}}$

A charge $q$ subject to a magnetic vector potential $A$ at $\left(\mathbf{r},t\right)$ due to a point charge $q'$ which had a velocity $\frac{∂\mathbf{r'}}{∂t}$ at $\left(\mathbf{r'},t'\right)$ has a potential momentum of:

q A (r, r^{'}) = φ (r, r^{'}) \underset{c o n s t a n t}{\frac{q}{c^{2}}} \underset{d i s l o c a t i o n}{\frac{\partial r^{'}}{\partial t}}

$q\mathbf{A}\left(\mathbf{r},\mathbf{r'}\right) \quad = \quad \varphi\left(\mathbf{r},\mathbf{r'}\right) \quad \underset{constant}{\frac{q}{c^2}} \quad \underset{dislocation}{\frac{∂\mathbf{r'}}{∂t}}$

q A (r, r^{'}) = \underset{c o n s t a n t}{\frac{μ_{0} q q^{'}}{4 π}} \underset{p r o x i m i t y}{\frac{1}{| r - r^{'} |}} \underset{d i s l o c a t i o n}{\frac{\partial r^{'}}{\partial t}}

$q\mathbf{A}\left(\mathbf{r},\mathbf{r'}\right) \quad = \quad \underset{constant}{\frac{\mu_0\ qq'}{4\pi}} \quad \underset{proximity}{\frac{1}{|\mathbf{r}-\mathbf{r'}|}} \quad \underset{dislocation}{\frac{∂\mathbf{r'}}{∂t}}$

Lorentz Force for $(q,q')$

The Lorentz Force between charges $(q,q')$ can be derived from the scalar potential $\varphi$ and the vector potential $\mathbf{A}$ .

A charge $q$ which has a velocity of $\mathbf{v}$ at $\left(\mathbf{r},t\right)$ will experience a Lorentz force due to a point charge $q'$ at $\left(\mathbf{r'},t'\right)$ of:

F = q [E + v \times B]

$\mathbf{F} \quad = \quad q\left[\mathbf{E} + \mathbf{v} \times \mathbf{B}\right]$

The electric field $\mathbf{E}$ is:

E = - \nabla φ - \frac{\partial A}{\partial t}

$\mathbf{E} \quad = \quad - \nabla \varphi - \frac{∂\mathbf{A}}{∂t}$

The magnetic field $\mathbf{B}$ is:

B = \nabla \times A

$\mathbf{B} \quad = \quad \nabla \times \mathbf{A}$

The Lorentz Force can be expressed directly in terms of the potentials:

F = q [- \nabla φ - \frac{\partial A}{\partial t} + v \times (\nabla \times A)]

$\mathbf{F} \quad = \quad q\left[- \nabla \varphi - \frac{∂\mathbf{A}}{∂t} + \mathbf{v} \times \left( \nabla \times \mathbf{A} \right)\right]$

Where:

$-\nabla \varphi$ = negative the gradient of the scalar potential $\varphi$ .
$-\frac{∂\mathbf{A}}{∂t}$ = negative the partial derivative of the magnetic vector potential $\mathbf{A}$ with respect to time $t$ .
$\mathbf{v} \times \left( \nabla \times \mathbf{A} \right)$ = the cross product of the velocity $\mathbf{v}$ of the charge $q$ and the curl of the magnetic vector potential $\nabla \times \mathbf{A} = \mathbf{B}$ due to charge $q'$ .

To restate from a previous section, the magnetic vector potential from a charge $q'$ at the position $\mathbf{r}$ at $q$ is:

A (r, r^{'}) = \underset{c o n s t a n t}{\frac{μ_{0} q^{'}}{4 π}} \underset{p r o x i m i t y}{\frac{1}{| r - r^{'} |}} \underset{d i s l o c a t i o n}{\frac{\partial r^{'}}{\partial t}}

$\mathbf{A}\left(\mathbf{r},\mathbf{r'}\right) \quad = \quad \underset{constant}{\frac{\mu_0\ q'}{4\pi}} \quad \underset{proximity}{\frac{1}{|\mathbf{r}-\mathbf{r'}|}} \quad \underset{dislocation}{\frac{∂\mathbf{r'}}{∂t}}$

Using the product rule, the partial derivative of this with respect to time $t$ can be found. For example, the derivative of a product of two variables $x$ and $y$ with respect to time $t$ is:

\frac{d}{d t} (x y) = \frac{d x}{d t} y + x \frac{d y}{d t}

$\frac{d}{dt}(xy) = \dfrac{dx}{dt}y + x\dfrac{dy}{dt}$ .

Therefore, the partial derivative of the magnetic vector potential at $\mathbf{r}$ due to $q'$ with respect to time $t$ is:

\frac{\partial A (r, r^{'})}{\partial t} = \underset{c o n s t a n t}{\frac{μ_{0} q^{'}}{4 π}} [\underset{p r o x i m i t y}{\frac{\partial [\frac{1}{| r - r^{'} |}]}{\partial t}} \underset{d i s l o c a t i o n}{\frac{\partial r^{'}}{\partial t}} + \underset{p r o x i m i t y}{\frac{1}{| r - r^{'} |}} \underset{d i s l o c a t i o n}{\frac{\partial [\frac{\partial r^{'}}{\partial t}]}{\partial t}}]

$\frac{∂\mathbf{A}\left(\mathbf{r},\mathbf{r'}\right)}{∂t} \quad = \quad \underset{constant}{\frac{\mu_0\ q'}{4\pi}} \left[ \underset{proximity}{ \frac{ ∂\left[ \frac{1}{|\mathbf{r}-\mathbf{r'}|} \right] }{∂t}} \quad \underset{dislocation}{\frac{∂\mathbf{r'}}{∂t}} + \underset{proximity}{\frac{1}{|\mathbf{r}-\mathbf{r'}|}} \quad \underset{dislocation}{ \frac{ ∂\left[ \frac{∂\mathbf{r'}}{∂t} \right] }{∂t}} \right]$

\frac{\partial A (r, r^{'})}{\partial t} = \underset{c o n s t a n t}{\frac{μ_{0} q^{'}}{4 π}} [\underset{p r o x i m i t y}{\frac{\partial [\frac{1}{| r - r^{'} |}]}{\partial t}} \underset{d i s l o c a t i o n}{\frac{\partial r^{'}}{\partial t}} + \underset{p r o x i m i t y}{\frac{1}{| r - r^{'} |}} \underset{d i s l o c a t i o n}{\frac{\partial^{2} r^{'}}{\partial t^{2}}}]

$\frac{∂\mathbf{A}\left(\mathbf{r},\mathbf{r'}\right)}{∂t} \quad = \quad \underset{constant}{\frac{\mu_0\ q'}{4\pi}} \left[ \underset{proximity}{ \frac{ ∂\left[ \frac{1}{|\mathbf{r}-\mathbf{r'}|} \right] }{∂t}} \quad \underset{dislocation}{\frac{∂\mathbf{r'}}{∂t}} + \underset{proximity}{\frac{1}{|\mathbf{r}-\mathbf{r'}|}} \quad \underset{dislocation}{ \frac{∂^2r'}{∂t^2} } \right]$

First term in the brackets
$\frac{ ∂\left[ \frac{1}{\|\mathbf{r}-\mathbf{r'}\|} \right] }{∂t}$ The partial derivative, with respect to time $t$ , of the proximity of the position $\mathbf{r}$ of $q$ at time $t$ to the position $r'$ of $q'$ at the retarded time $t' = t - \|\mathbf{r}-\mathbf{r'}\|/c$ .	$\frac{∂r'}{∂t}$ According to an observer at time $t$ : the velocity a charge $q'$ had at the retarded time $t' = t - \|\mathbf{r}-\mathbf{r'}\|/c$ , when it emitted a light signal which has now reached $q$ at position $\mathbf{r}$ and time $t$

Second term in the brackets
$\frac{1}{\|\mathbf{r}-\mathbf{r'}\|}$ The proximity of the position $\mathbf{r}$ of $q$ at time $t$ to the position $r'$ of $q'$ at the retarded time $t' = t - \|\mathbf{r}-\mathbf{r'}\|/c$ .	$\frac{∂^2r'}{∂t^2}$ According to an observer at time $t$ : the acceleration a charge $q'$ had at the retarded time $t' = t - \|\mathbf{r}-\mathbf{r'}\|/c$ , when it emitted a light signal which has now reached $q$ at position $\mathbf{r}$ and time $t$